总结

对于这些内容接下来会一一解释
向量之间的正交

空间之间的正交
Def: 两个空间相互正交,即在这两个空间中,分别取任意一个向量,这两个向量都正交
Ex: 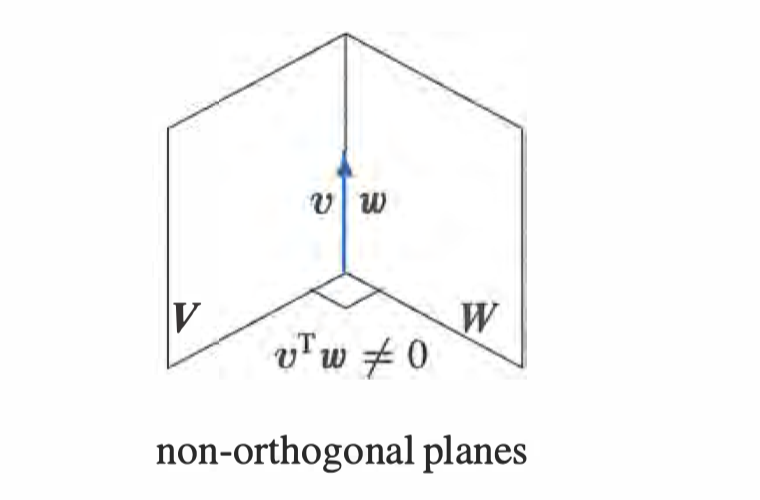
正交补空间
直观上:子空间\(U\)和正交补空间\(U^{\perp}\)的和构成了整个空间,即该空间中的一个向量可以分解为\(U\)中的一个向量加上\(U^\perp\)中的一个向量。
若\(U\)和\(U\perp\)都为\(R^n\)的子空间,则有以下性质
- \(dimU + dimU^\perp = n\)
四个子空间之间的关系
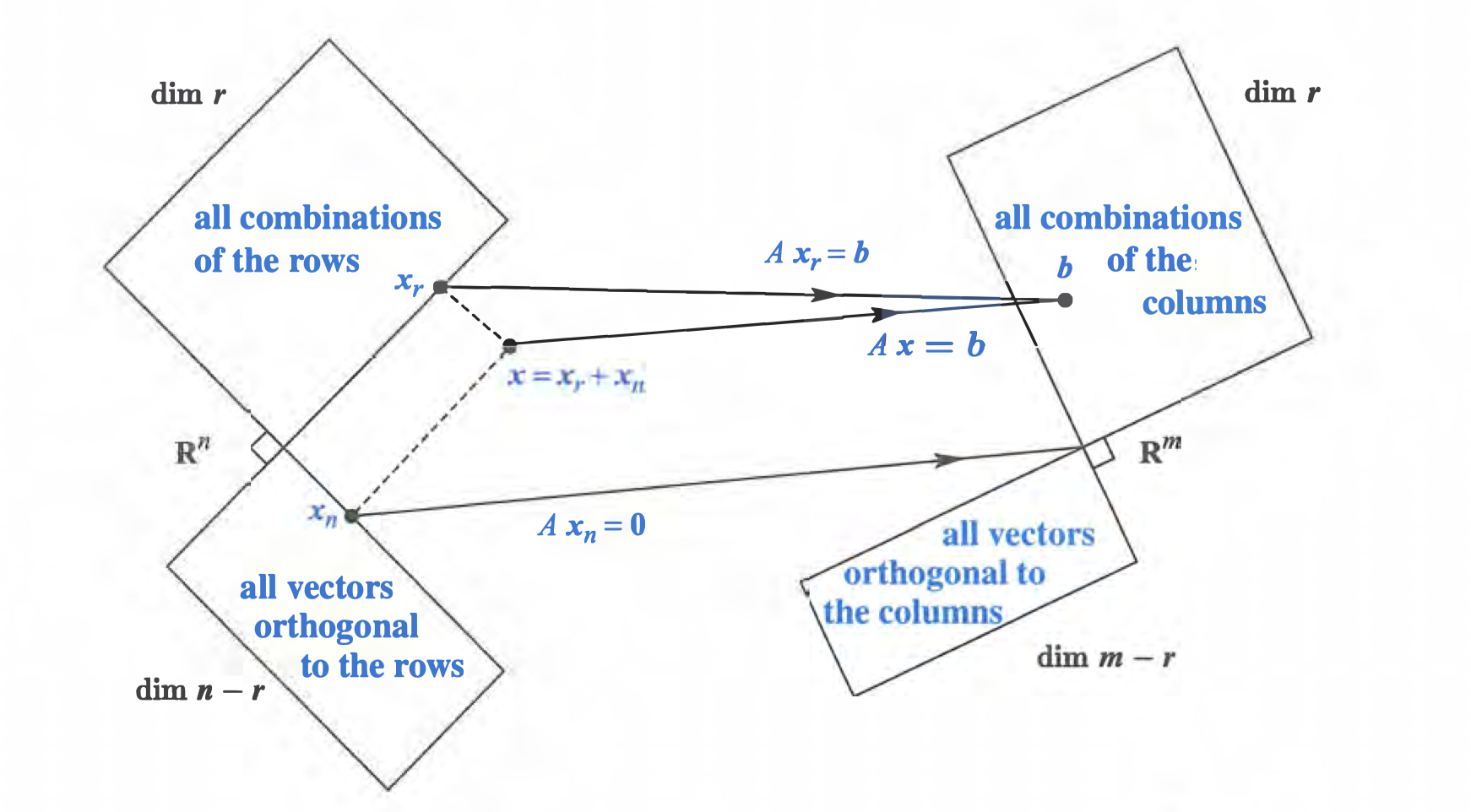
- 列空间和左零空间相互正交
- 行空间和零空间相互正交
- 方程\(Ax=b\)中的x位于\(R^n\)空间中
- 若矩阵A可逆,行空间中的所有向量与列空间中的向量一一对应
第二点的证明如下:

- 每一行与零空间的向量的点乘都为0
- 每个行向量之间的线性组合与零空间的点乘也为0 -> 线性组合构成行空间中的任意一个向量
除此之外可以用代数的方法证明:
\[x^T(A^T y) = (Ax)^T y = 0\]
第三第四点证明如下:
第三点很显然,因为x有n个分量,肯定在\(R^n\)中,根据正交补空间的性质,x就可以分解为\(x = x_{row} + x_{null}\)
故 \[Ax = A(x_{row} + x_{null}) = Ax_{row} + 0\]
当矩阵A不可逆的时候是做不到列空间中的向量与行空间中的向量一一对应的,因为存在着零空间的分量。但是当可逆的时候,零空间只有0。