投影(Projection)
概要

投影矩阵、投影、误差向量
目标: 找出向量b在空间S上的投影p,以及产生p的矩阵P
误差向量: \(e = b - p = A \hat x\)
tips: A 是空间 S 的基向量构成的矩阵
方法: 根据几何关系可以得到\(e\)与空间S正交。描述一个空间的最好方法就是用基向量描述,把基向量放入矩阵A中,该矩阵的列空间即为空间S,由\(e \perp S\),得到\(e \in LN(S)\),即误差向量在S的左零空间中。
下图是图例: 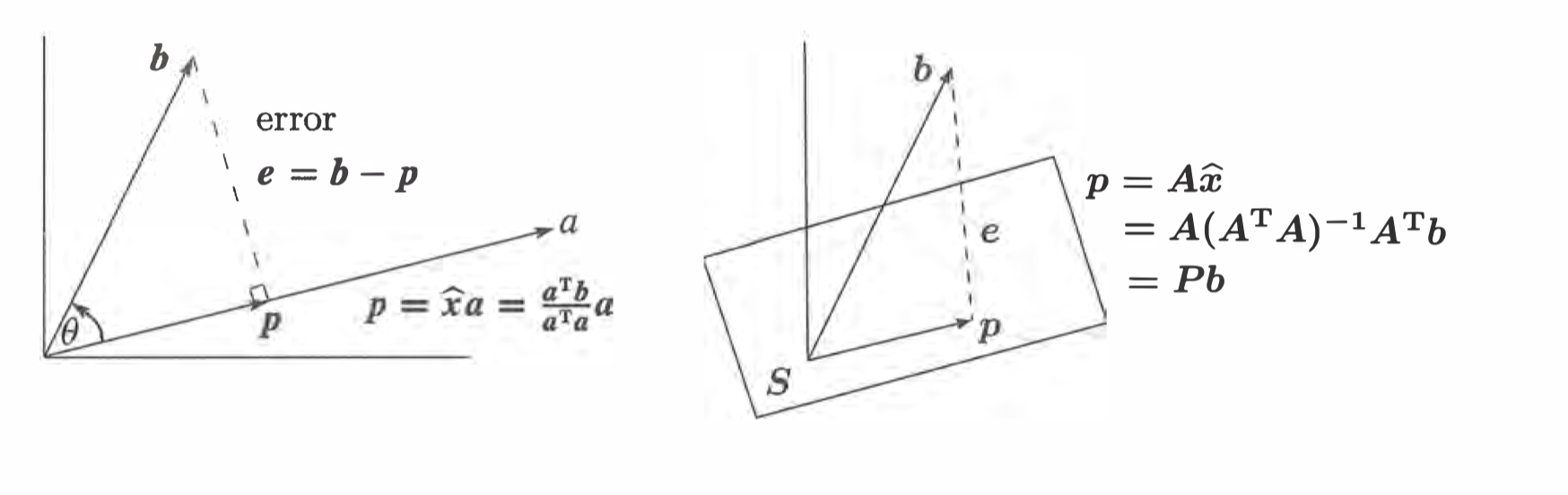
由上述关系可得:
\[ \begin{aligned} A^\top (b - A\hat x) &= 0 \\ \hat x &= (A^\top A)^{-1}A^\top b \\ p &= Ax = A(A^\top A)^{-1}A^\top b \\ P &= A(A^\top A)^{-1}A^\top \end{aligned} \]
最小二乘法(Least Squares)
目的: \(Ax = b\)有时候无解,我们为了找到最接近的(误差最小的解),可以去解\(A\hat x=p\),其中\(b = p + e\)
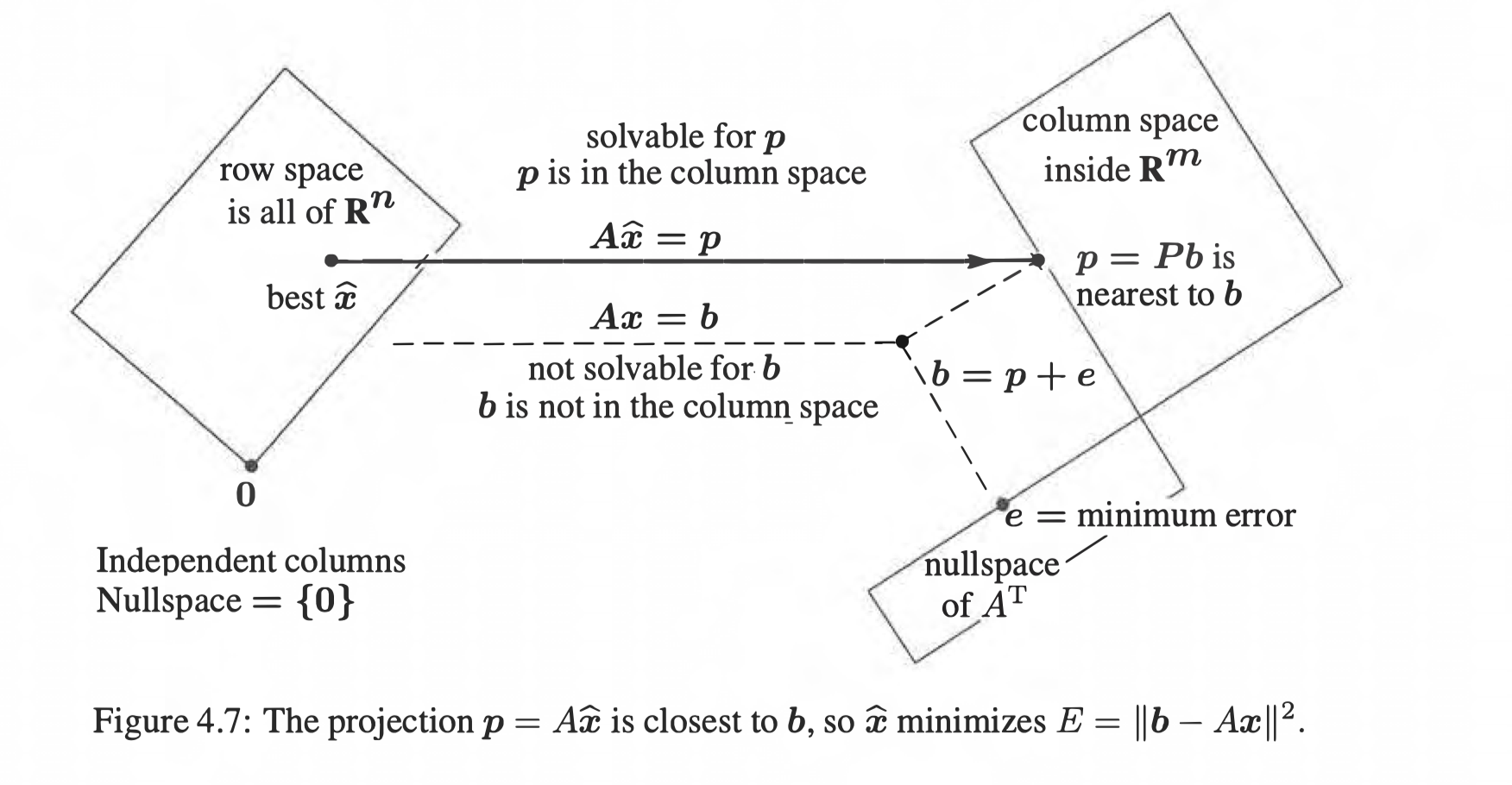
上图是最直观的一幅图,有以下几点需要注意
- A是线性无关的列构成的矩阵,所以其零空间只有0
- 因为列空间和左零空间互为正交补空间,所以b能分解为\(p+e\)
- 将b投影到p的投影矩阵是P,而投影到e的投影矩阵是I-P
第三点的证明:
我们已知\(b = p + e\),而\(p = Pb\),简单代数运算后得到\(e = (I-P)b\),然后再证明e在A的左零空间中.
\[ \begin{aligned} P &= A (A^T A)^{-1} A^T \\ A^T P &= A^T \bigl(A (A^T A)^{-1} A^T \bigr) \\ &= (A^T A)(A^T A)^{-1} A^T \\ &= A^T \\ A^T(I-P) &= A^T - A^T P = 0 \\ A^T(I-P)\mathbf b &= 0 \\ \end{aligned} \]
另一个证明:
\[ \begin{aligned} e &= b - p \\ Pe & = P(b - p)\\ &= p - p \\ & = 0 \end{aligned} \] ## \(A^TA\)的可逆性证明
前提条件: A的列向量是线性无关的
proof: 要证\(A^TA\)可逆,即证\(A^TAx=0\)的解只有零向量 \[ \begin{aligned} suppose: A^TAx &= 0 \\ x^TA^TAx &=0 \\ (Ax)^TAx &=0 \\ Ax = 0 \\ \end{aligned} \]
最后得到只需要证明\(Ax=0\),但我们的前提条件是A的列向量之间是线性无关的,所以证毕
补充
- 若b在子空间S中,则\(Pb = b\)。反之也成立。
- 若b垂直于子空间S,则\(Pb = 0\)。反之也成立。
第一条证明:
因为b在子空间S中,所以b为列向量的线性组合,即\(b = Ax\) \[ \begin{aligned} P &= A(A^TA)^{-1}A^T \\ Pb &= A(A^TA)^{-1}A^Tb \\ &= A(A^TA)^{-1}A^TAx \\ &= A(A^TA)^{-1}(A^TA)x \\ &= Ax \\ &= b \\ \end{aligned} \]
第二条证明:
因为b垂直于子空间S,则\(b \in S^\perp\),所以\(A^Tb = 0\)
\[ \begin{aligned} P &= A(A^TA)^{-1}A^T \\ Pb &= A(A^TA)^{-1}A^Tb \\ &= 0 \end{aligned} \]